Ecco un paradosso tratto dal libro "Ah! Ci sono!" di Martin Gardner:
Un ricco avvocato possedeva 11 automobili d’epoca, ciascuna del valore di circa 25000 dollari. Alla sua morte, lascia un curioso testamento in cui si chiede che le sue 11 macchine siano divise tra i suoi tre figli: metà al maggiore, un quarto al secondo e un sesto al più giovane. Tutti rimangono perplessi. Come si fa a dividere 11 macchine in due parti uguali? O in quattro parti? O in sei parti? Mentre i figli stanno discutendo sul da farsi, arriva la dottoressa Zero, famosa numerologa, alla guida della sua nuova macchina sportiva.
Dr. Zero: Salve ragazzi. Mi sembra che abbiate un problema. Posso esservi d’aiuto?
Dopo che i figli hanno spiegato la situazione, la dottoressa Zero parcheggia la sua auto sportiva vicino alle 11 macchine d’epoca e salta giù.
Dr. Zero: Ditemi, ragazzi, quante macchine ci sono? I ragazzi ne contano 12.
Allora la dottoressa Zero esegue i termini del testamento e dà al maggiore metà delle macchine, cioè 6, al secondo ne dà un quarto, cioè 3, e al minore un sesto, cioè 2.
Dr. Zero: 6 più 3 più 2 fa esattamente 11. Così rimane un’automobile, la mia.
La dottoressa Zero salta sulla sua macchina sportiva e se ne va.
Dr. Zero: Sempre lieta di aiutarvi, ragazzi! Vi manderò la mia parcella!
(Nota di Fabio: Il paradosso sta nel fatto che 1/2 + 1/4 + 1/6 NON è uguale a 1, quindi il testamento non divide l’intero ammontare delle auto e bisogna quindi arrotondare per ottenere un numero intero di auto per ciascun erede)
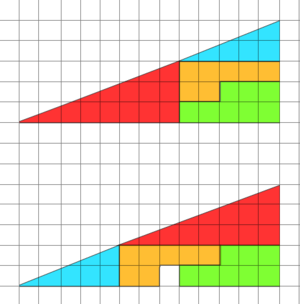
(Ora guardate la figura: il prima triangolo è composta da 4 figure, le stesse identiche del secondo triangolo. E allora come è possibile che ci sia un qudratino in più? La risposta la trovate qui)
